Найдите третий член геометрической прогрессии 6 3

Арифметическая прогрессия: свойства и формулы
Геометрической прогрессией называется числовая последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число. Число называется знаменателем геометрической прогрессии. Например: 2, 6, 18, 54,… — возрастающая геометрическая прогрессия,. Любой член геометрической прогрессии может быть вычислен по формуле:. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних:. Сумма первых членов геометрической прогрессии обычно обозначается как и при вычисляется по формуле:.



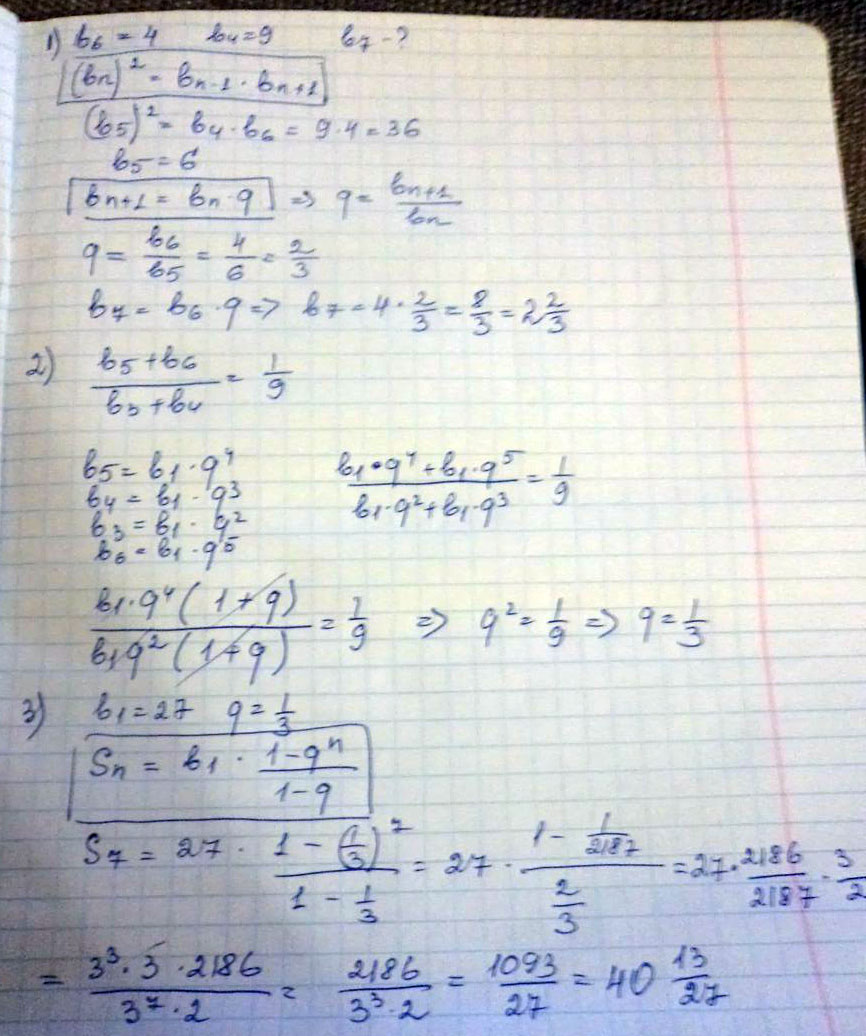


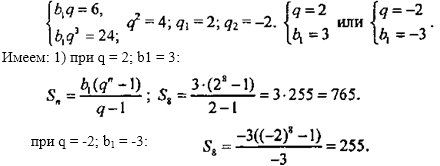




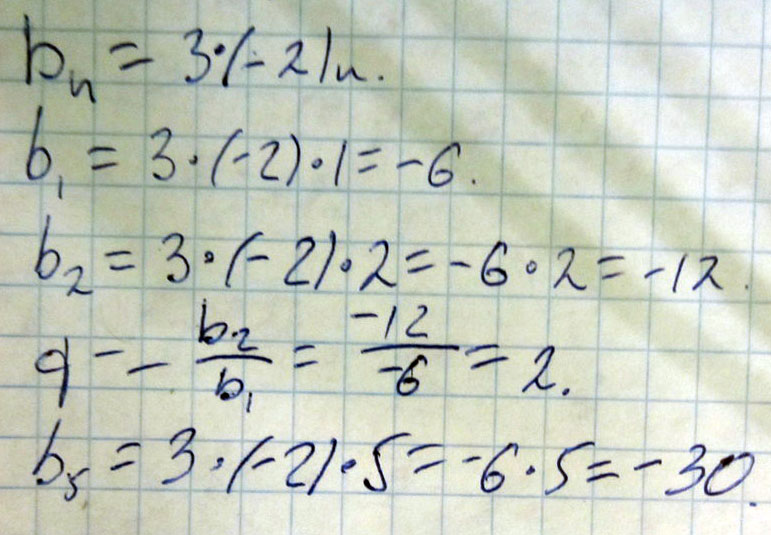

Найди третий член геометрической прогрессии, если b1 равно 6 q равно минус 2 Запиши число в поле ответа. Найди третий член геометрической прогрессии, если b1 равно шесть q равно минус два Запиши число в поле ответа. Информация для покупателей. Задача Найди третий член геометр Вы ввели [src].









Арифметической прогрессией a n называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d d — разность прогрессий. Геометрической прогрессией b n называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число q q — знаменатель прогрессии. Найдите двадцать второй член прогрессии. Найдите семьдесят пятый член этой прогрессии. Для арифметической прогрессии характеристическое свойство имеет вид. Найдите сумму семнадцати первых членов.